1008. Construct Binary Search Tree from Preorder Traversal - medium
문제
Return the root node of a binary search tree that matches the given preorder traversal.
(Recall that a binary search tree is a binary tree where for every node, any descendant of node.left has a value < node.val, and any descendant of node.right has a value > node.val. Also recall that a preorder traversal displays the value of the node first, then traverses node.left, then traverses node.right.)
제한사항
- 1 <= preorder.length <= 100
- The values of preorder are distinct.
입출력 예
1
2
3
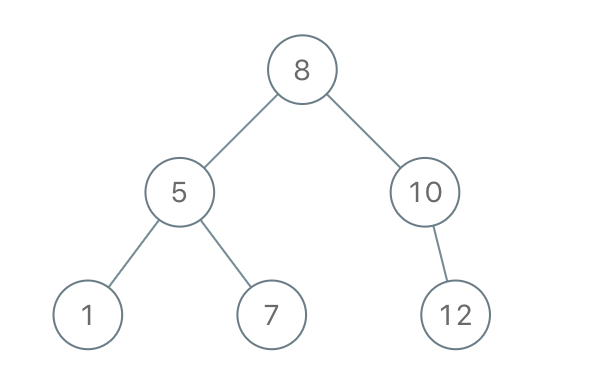
Example 1:
Input: [8,5,1,7,10,12]
Output: [8,5,10,1,7,null,12]
풀이
- Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
// start index의 값보다 큰 값의 index 리턴
int getMaxIndex(vector<int>& preorder, int start, int last){
for(auto i = start + 1 ; i < last ; ++i){
if(preorder[i] > preorder[start]){
return i;
}
}
// start index보다 큰 값이 없으면 last 리턴
return last;
}
TreeNode* createNode(vector<int>& preorder, int start, int last){
// start와 last가 같다는것은 이후 노드가 없다는 뜻
if(start == last)
return nullptr;
TreeNode* node = new TreeNode(preorder[start]);
auto maxIndex = getMaxIndex(preorder, start, last);
// start가 maxIndex보다 작다는 것은,
// start와 last사이에 start의 값보다 작은 수가 있다는 뜻이므로,
// 이는 left child 노드의 후보가 됨
if(start < maxIndex)
node->left = createNode(preorder, start + 1, maxIndex);
// maxIndex가 last보다 작다는 것은,
// maxIndex가 last사이에 maxIndex의 값보다 큰 수가 있다는 뜻이므로,
// 이는 right child 노드의 후보가 됨
if(maxIndex < last)
node->right = createNode(preorder, maxIndex, last);
return node;
}
TreeNode* bstFromPreorder(vector<int>& preorder) {
TreeNode* head = createNode(preorder, 0, preorder.size());
return head;
}
};
