LeetCode - 1007. Minimum Domino Rotations For Equal Row

1007. Minimum Domino Rotations For Equal Row - medium

문제

In a row of dominoes, A[i] and B[i] represent the top and bottom halves of the i-th domino. (A domino is a tile with two numbers from 1 to 6 - one on each half of the tile.)

We may rotate the i-th domino, so that A[i] and B[i] swap values.

Return the minimum number of rotations so that all the values in A are the same, or all the values in B are the same.

If it cannot be done, return -1.

제한사항

• 1 <= A[i], B[i] <= 6
• 2 <= A.length == B.length <= 20000

입출력 예

Example 1:

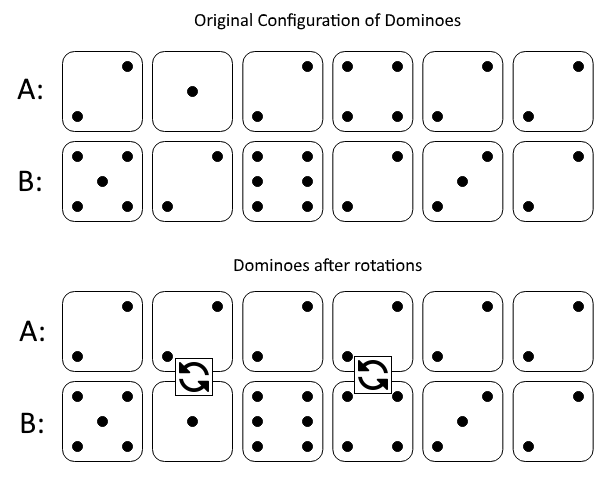
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
Explanation: 
The first figure represents the dominoes as given by A and B: before we do any rotations.
If we rotate the second and fourth dominoes, we can make every value in the top row equal to 2, as indicated by the second figure.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
Explanation: 
In this case, it is not possible to rotate the dominoes to make one row of values equal.

풀이

• Arrary, Hash

class Solution {
public:
    int minDominoRotations(vector<int>& A, vector<int>& B) {
        int ans = INT_MAX;
        int n = A.size();
        
        // map의 key를 주사위눈으로 하고, 
        // value를 해당 주사위눈을 값으로 가지는 A,B의 index와,
        // 해당 index가 A,B중 어느 vector의 index인지 혹은 둘다 가지고 있는지 표기하는 값으로로 함.
        // 즉, A,B vector 끼리 바꿀시 해당 주사위눈으로 모두 만들때,
        // 결국 0 ~ n 까지 모든 index가 map의 key에 해당하는 주사위눈의 value에 모두 존재해야함
        map<int, vector<pair<int,char>>> m;
        
        // vector를 한번 조회하여 map을 구성
        for(auto i = 0 ; i < n ; ++i){
            // 만약 해당 주사위눈에 대한 값이 서로 같은 index에 있으면 'S' 로 표기
            if(A[i] == B[i])
                m[A[i]].push_back({i, 'S'});
            // 서로의 각 i index에 해당하는 주사위눈에 대한 index와 'A', 'B'를 각각 표기 
            else {
                m[A[i]].push_back({i, 'A'});
                m[B[i]].push_back({i, 'B'});
            }
        }
        
        // 완성된 map을 조회
        for(auto i : m){
            // 현재 key의 주사위눈이 가지는 값이 A,B vector의 크기와 같다면,
            // A,B vector의 서로 원소 스왑으로 해당 주사위눈만 가지는 vector를 만들수 있다는 뜻
            if(i.second.size() == n){
                map<char, int> counting;
                
                // 기록된 표기별 카운팅
                for(auto j = i.second.begin() ; j != i.second.end() ; ++j)
                    ++counting[j->second];
                
                // A 기반으로 스왑하는게 더 적은수인지, 혹은 B 기반으로 스왑하는게 더 적은수인지 계산
                // 이때 서로 겹치게 되는 'S'의 수를 별도로 빼줌
                auto swapCount = (n - max(counting['A'], counting['B'])) - counting['S'];
                
                // 최소값 비교
                ans = min(ans, swapCount);
            }
        }
        
        return ans != INT_MAX ? ans : -1;
    }
};