소프트웨어 시스템에서 시간의 주요 사용 사례 중 하나는 다양한 이벤트의 순서를 결정하는 것이다.
중앙 집중형과 분산 시스템에서 이벤트의 순서를 지정하는데 있어 시계의 존재에 대해서 차이가 존재한다.
중앙집중형에는 노드가 하나뿐 이므로 시계도 하나뿐이다. 이는 보편적으로 단일한 시간 차원을 유지할 수 있기때문에 단일 노드에서의 다양한 이벤트의 순서를 결정 할 수 있다.
반면 분산 시스템에서는 각 노드마다 자체 시계가 존재한다. 즉, 분산 시스템에서는 여러 노드에서 발생하는 이벤트의 순서를 지정할 글로벌 시계가 존재하지 않는다.
그러므로 분산 시스템을 구축할 때 시계 간의 차이를 고려해야 한다. 전체 시스템은 이러한 모든 시계가 동일하고 단일 글로벌 시계로 작동한다는 가정 하에서 작동해서는 안된다.
논리적 시게
논리적 시계는 시간을 추적하기 위해 물리적 프로세스에 의존하지 않는 시계의 대체 범주이다. 대신 시스템 노드 간에 교환되는 메시지를 활용한다. 이는 앞서 논의한 바와 같이 분산 시스템 에서 정보 흐름의 주요 메커니즘이기도 하다.

Total and Partial Ordering
이벤트 순서를 결정하는 것은 소프트웨어 시스템에서 해결해야 하는 일반적인 문제이다. 그러나 순서에는 전체 순서과 부분 순서라는 두가지 다른 유형의 순서가 있다.
전체 순서(Total Ordering)
전체 순서 는 집합의 두 요소를 서로 비교하는 이진 관계이다. 이 관계를 사용하여 집합의 모든 요소에 대해 단일 순서만 파생할 수 있다. 이것이 바로 전체 주문 이라고 불리는 이유입니다.
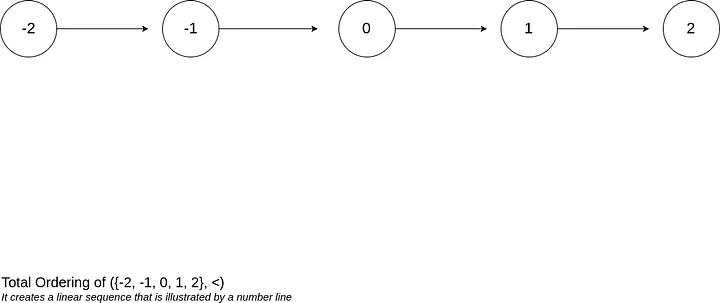
단일 노드로 구성된 시스템에서는 이벤트의 전체 순서를 결정하는 것이 쉽고 직관적이다. 주된 이유는 모든 이벤트가 발생하는 단일 액터가 있으므로 이 액터가 이러한 이벤트가 발생할 때 전체 순서를 부과할 수 있기 때문이다.
부분 순서(Partial Ordering)
부분 순서 는 집합의 일부 요소만 서로 비교하는 데 사용할 수 있는 이진 관계이다. 이 관계를 사용하여 집합의 모든 요소에 대해 여러 개의 유효한 순서를 도출할 수 있습니다.
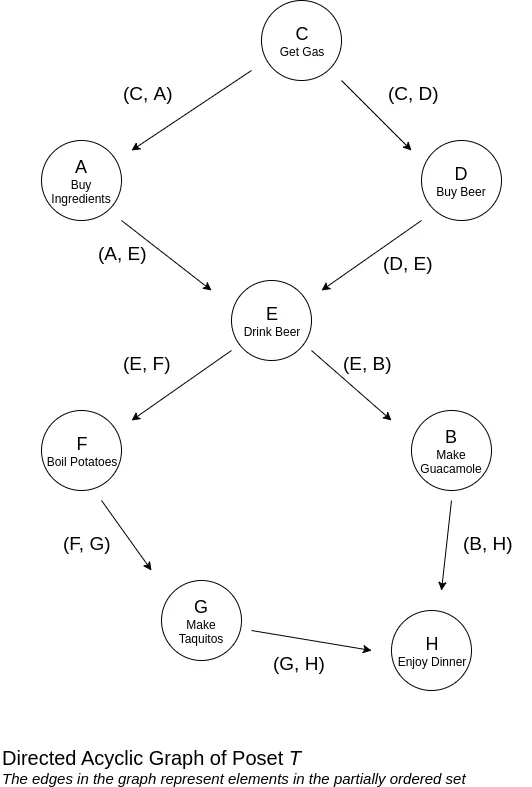
분산 시스템에는 여러 노드가 있고 이벤트가 여러 노드에서 동시에 발생할 수 있기 때문에 전체 순서가 꼭 필요하지 않은 경우 발생하는 이벤트의 유효한 부분 순서를 사용할 수 있다.
Lamport Clocks
램포트 시계에서의 논리 시계는 시스템의 모든 노드가 작동을 시작할 때 0부터 시작하는 숫자 카운터 형태의 논리 시계를 유지한다.
프로토콜의 규칙은 아래와 같다.
- [R1]이벤트(전속, 수신, 로컬)를 실행 하기 전에 노드는 논리 시계의 카운터를 1 증가 시킨다.
- $C_i = C_i + 1$
- [R2]전송된 모든 메시지는 전송 시간에 보낸 사람의 시계 값을 피기백하고 노드는 타임스탬프 값이 있는 메세지를 받고 다음 작업을 실행한다.
- 시계와 수신된 시계의 최대값을 사용하여 시계를 업데이트 함
- $C_i = max(C_i, C_m)$
- R1을 실행
- 메세지를 전달
- 시계와 수신된 시계의 최대값을 사용하여 시계를 업데이트 함

Lamport 시계 는 서로 다른 노드의 시계가 동일한 값(예: 노드 ID)을 갖는 경우 연결을 끊는 임의의 메커니즘을 사용하여 분산 시스템에서 이벤트의 전체 순서를 생성하는 데 사용할 수 있다.
주의할 점은 이 전체 순서가 다소 임의적이며 인과 관계를 추론할 수 없다는 것이다. 이는 Lamport 시계가 가질 수 있는 실제 응용 프로그램의 수를 제한한다.
Vector Clocks
Lamport 시계의 주요 한계 는 강력한 클럭 조건을 충족하지 못한다는 것이다. 이는 사건 간의 인과 관계를 추론하는 데 사용할 수 없음을 의미한다.
따라서 우리는 각 사건보다 먼저 발생하는 모든 사건의 집합을 유지해야 한다.
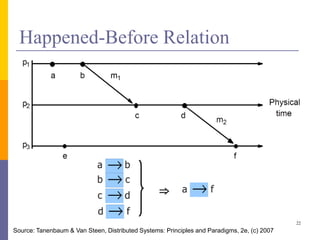
벡터 클럭 은 논리 클럭의 또 다른 유형으로, 각 노드의 클럭 데이터 구조는 다음의 벡터입니다.
- 시스템의 노드의 수 $N$ 만큼 clock의 벡터 $[c^0, c^1, …c^N]$ 구성
프로토콜의 규칙은 아래와 같다.
- [R1]이벤트(전속, 수신, 로컬)를 실행 하기 전에 노드는 논리 시계의 카운터를 1 증가 시킨다.
- $C^i_i = C^i_i + 1$
- [R2]전송된 모든 메시지는 전송 시간에 보낸 사람의 시계 값을 피기백하고 노드는 벡터 $[c^0_j, c^1_j, …c^N_j]$ 가 포함된 메세지를 받고 다음 작업을 실행한다.
- R1을 실행
- 자체 벡터 시계값과 수신된 메세지의 벡터 값중 최대값을 취하여 벡터의 각 요소를 업데이트
- $C^k_i = max(C^k_i, C^k_j)$, $k$ in $[0, N]$
- 메세지를 전달
벡터 클록은 두 이벤트가 인과적으로 연관되어 있는지 또는 동시에 발생하는지 감지하는 기능의 이점을 누릴 경우 사용할 수 있다. 또한 시스템의 다양한 노드가 동기화 및 조정 병목 현상 없이 독립적이고 효율적으로 진행할 수 있도록 해준다.
참고

